quinta-feira, 8 de outubro de 2015
segunda-feira, 28 de setembro de 2015

Eclipse da Superlua
Finalmente chegou o dia! Neste domingo teremos a segundaSuperlua, das três que acontecem no ano, mas que vem com um bônus: será dia de eclipse lunar também! Desta vez o Brasil estará em situação privilegiada para acompanhar o evento, que também deve ser visto na costa oeste da África e Europa, mas também na costa leste dos EUA, mesmo que parcialmente.
E o papo é o seguinte:
O que tem de especial em um eclipse com uma Superlua?
Não é muito comum acontecer os dois eventos ao mesmo tempo. A Superlua se dá quando a Lua atinge a fase de cheia a menos de 24 horas do seu ponto mais próximo da Terra em sua órbita, ponto esse conhecido como perigeu. Esse ano nós já tivemos uma Superlua em agosto, teremos outra agora em setembro e finalmente a última em outubro. Ainda que na prática seja muito difícil de ver diferenças entre as três, a melhor delas é sem dúvida a de domingo agora, dia 27.
Quando a Lua Cheia ocorre no perigeu, ela surge com o tamanho aparente maior, até 14% e até 30% mais brilhante. Esse tamanho mais avantajado é pouco notado quando ela está alta no céu, pois falta alguma coisa perto da Lua para comparar, mas quando ela surge no horizonte, parece bem maior que normalmente estamos acostumados a ver. Ela fica mais brilhante também, o que dá para notar, mesmo dentro de cidades grandes, mas que chega a impressionar se estivermos em um local escuro.
Aí tem um eclipse nessa Lua do Perigeu (o nome oficial da Superlua) e fica tudo de bom! Quando a Lua mergulhar na sombra da Terra, veremos um contraste entre as fases brilhante e escura ainda maior que o normal, bombando os efeitos do eclipse. A última vez que um eclipse aconteceu numa Superlua foi há mais de 30 anos e a próxima só deve acontecer daqui a 17 anos.
O quê eu preciso para ver o eclipse?
Duas coisas: céu limpo e horizonte aberto! Esse é um dos eventos astronômicos em que não é preciso nenhum tipo de equipamento, basta que o céu esteja limpo e que você consiga ver a Lua no céu. Claro que a festa fica ainda melhor se houver uma luneta ou telescópio disponível. Nesse caso dá para ver a sombra da Terra percorrendo a superfície lunar, cobrindo as crateras, vales e montanhas conforme a Lua e a Terra se movimentam. Se você for que nem eu que gosta de ficar horas contemplando o céu, sugiro usar uma cadeira de praia ou espreguiçadeira para fiar mais confortável.
Qual o horário do eclipse?
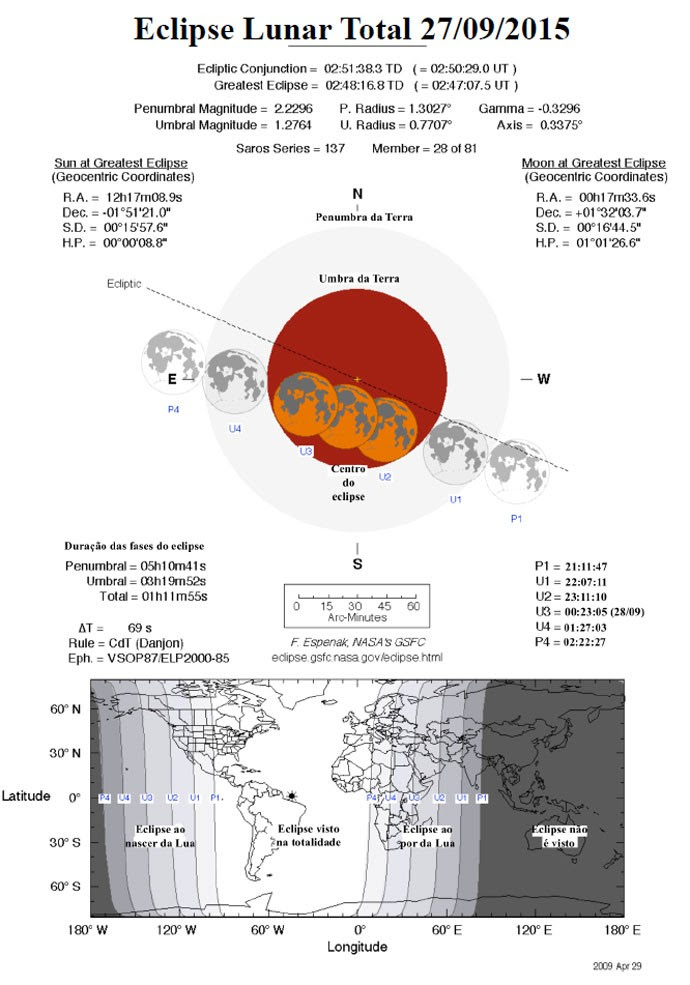
O eclipse lunar total, como é esse caso, é composto de duas fases: a penumbral e a umbral. A sombra da Terra tem um halo externo mais tênue, a penumbra, e uma parte bem mais escura ao centro, a umbra. Como o eclipse é total, a Lua vai mergulhar totalmente em ambas durante seu trajeto no céu.
Durante a fase penumbral, a Lua escurece um pouco e às vezes até passa despercebido de tão sutil. Apenas observadores mais atentos conseguem distinguir o começo dessa fase, quando a borda da Lua toca a penumbra da Terra (evento chamado de P1 às 21:11), mas conforme ela vai se deslocando sobre ela, o escurecimento fica mais evidente.
A segunda fase é a umbral. Aí sim fica evidente que a Lua está sendo coberta pela sombra densa da Terra. Quando há o primeiro toque da borda da superfície lunar com a umbra (evento chamado de U1, às 22:07), parece que ela perdeu um pedaço de tão escuro que fica e conforme a sombra avança, o pedaço aumenta junto. Quando a Lua estiver completamente coberta pela umbra, começando a fase de totalidade no instante U2 (23:11) vai ficar bem evidente a mudança de sua cor, pois ela deve ficar um tanto mais alaranjada.
Mesmo quando a Lua está mergulhada na umbra da Terra, um pouco da luz do Sol consegue atingi-la, após atravessar a atmosfera da Terra. O efeito de mudança da cor tem a ver com o estado da atmosfera terrestre. A luz, ao atravessa-la, vai ser influenciada por tudo que ela contém. Logo de cara, a pouca luz que chega na Lua vai ser um pouco alaranjada, simplesmente por que a parte azul dela é muito espalhada pela nossa atmosfera. Por isso o céu é azul. Mas se ela estiver carregada com particulados como poeira e, principalmente, cinzas vulcânicas, esse efeito é acentuado e praticamente apenas luz vermelha vai atingir a Lua. Recentemente tivemos duas erupções vulcânicas intensas que lançaram cinzas na alta atmosfera. Nessa região de altitude elevada, as cinzas podem circular por anos antes de caírem de volta ao solo, de modo que espera-se que esse efeito de avermelhar a Lua seja bem destacado nesse eclipse.
A fase da totalidade dura até o momento em que a Lua começa a sair da umbra (instante U3, 00:23 de segunda feira 28) e volta a mergulhar na penumbra. Essa fase deve durar um pouco mais do que 1 hora e 10 minutos e durante esse tempo aLua deverá estar mais obscurecida e avermelhada, dependendo da situação da atmosfera terrestre.
Existe uma escala proposta pelo astrônomo francês Andrés-Louis Danjon para quantificar o grau de escuridão que a Luaatinge nesses momentos de eclipse total. A escala de Danjon varia de 0 (muito escuro, quase invisível) até 4 (muito claro, cor alaranjada). Essa escala é bastante arbitrária, mas ela ajuda a revelar o grau de sujeira suspensa na atmosfera de acordo com o brilho e a cor da Lua.
Finalmente o eclipse termina quando a Lua toda sair da penumbra (P4), que deve acontecer às 02:22 da madrugada de segunda feira. Se você não pode se dar ao luxo de ficar acordado até duas da matina em plena segunda feira braba, tente ao menos ver a Lua atingir o ápice do eclipse, que deve ocorrer entre os pontos U2 e U3 e dura pouco mais do que uma hora.
Para organizar melhor as ideias, tem esse esquema do eclipse com muitos dados sobre todo o evento. O que mais interessa é a tabela com os horários de entrada e saída da sobra da Terra, sempre na hora oficial de Brasília.
Por quê algumas pessoas estão chamando o eclipse de “Lua sangrenta”?
Porque o mundo está recheado de pessoas bestas, se quer saber mesmo. Eu já falei sobre essa história de Luasangrenta nesse post e cada vez mais acho que esse termo deve ser evitado!
E se chover?
Aí o jeito é acompanhar o eclipse na internet. Vário sites vão fazer transmissão ao vivo do evento, um deles é esse da famosa revista Sky & Telescope. A transmissão começa às 22 horas do dia 27/09.
Um outro fato curioso desse eclipse, em especial para os fãs de Neil Young como eu, é que ele deve ocorrer justo na famosa “Harvest Moon”, ou Lua da Colheita. Muito antes da luz elétrica, a Lua Cheia que ocorria próximo ao equinócio que marca o fim do verão no norte era usada para dar mais algumas horas de luz após o Sol se por, com isso, a colheita não seria interrompida tão cedo. Fica aí uma dica de trilha sonora para o evento!
Então neste domingo temos um encontro marcado com a Lua, a Terra e o Sol, que alinhados vão nos oferecer um belo espetáculo.
Fonte: http://g1.globo.com/ciencia-e-saude/blog/observatorio/post/eclipse-da-super-lua.html
quarta-feira, 23 de setembro de 2015
Brasileiro na lanterna...
Alunos brasileiros estão na lanterna em ranking de habilidades digitais, diz OCDE
Estudo avaliou compreensão de leituras na internet e destreza para navegar em sites em jovens de 31 países; Cingapura fica em 1º lugar.
Daniela Fernandes Da BBC Brasil
Os alunos brasileiros estão nas últimas posições em um ranking de 31 países que avaliou a habilidade de navegar em sites e compreender leituras na internet elaborado pela Organização para a Cooperação e Desenvolvimento Econômico (OCDE).
O relatório Estudantes, Computadores e Aprendizado: Fazendo a Conexão, realizado no âmbito do Programa Internacional de Avaliação de Estudantes (PISA) da OCDE de 2012, resultou do primeiro estudo da organização que analisa as competências de alunos na área digital.
O Brasil ficou na antepenúltima posição no ranking, à frente apenas dos Emirados Árabes e da Colômbia.
Os melhores resultados foram obtidos pelos alunos de Cingapura, Coreia do Sul, Hong Kong, Japão, Canadá e Xangai.
Computador na escola
Os resultados desses países (ou cidades) refletem os que foram obtidos no PISA de 2012 para avaliação de leitura em papel, "o que parece indicar que um bom número de habilidades úteis para navegar na internet pode também ser ensinada e adquirida por meio de técnicas de leitura clássicas", diz a OCDE.
O estudo sugere que o acesso e uso de computador importa menos no desenvolvimento da capacidade de navegação e leitura online do que um bom preparo básico. Sugere também que a habilidade para navegar na internet pode ser ensinada e adquirida com a ajuda de pedagogias e ferramentas tradicionais.
Os dois primeiros do ranking, os alunos de Cingapura e da Coreia do Sul, utilizam menos computadores na escola - apenas 70% dos alunos usam computador, no caso de Cingapura, e 42% na Coreia do Sul - do que a média dos países da OCDE - de 72%. Não há esse dado sobre o Brasil no estudo.
Segundo a organização, "o fato de assegurar que cada aluno atinja um nível de competências de base em leitura e matemática contribuirá mais para a igualdade em um mundo digital do que o simples fato de ampliar ou subvencionar o acesso a serviços e aparelhos de alta tecnologia".
"A leitura online solicita as mesmas competências que a leitura em papel. No entanto, é preciso acrescentar uma capacidade suplementar, que não é das menores: a de saber navegar entre páginas de texto e discernir as fontes pertinentes e dignas de confiança entre um número de informações aparentemente infinito", afirma o estudo.
 Alunos que usaram computadores com muita frequência na escola tiveram resultados piores em leitura online (Foto: BBC Brasil)
Alunos que usaram computadores com muita frequência na escola tiveram resultados piores em leitura online (Foto: BBC Brasil)
Para avaliar as habilidades na internet, os alunos - de 15 anos - tiveram de navegar por textos online através de links, atalhos e comandos de navegação para ter acesso à informação solicitada, além de criar um gráfico a partir de dados ou utilizar calculadoras na tela do computador.
Os pesquisadores analisaram o número de etapas para buscar informações e também a capacidade para navegar de maneira focada na busca por determinados assuntos (clicando corretamente, por exemplo, na sequência de páginas que permitiam realizar a tarefa solicitada).
O documento revela que mesmo os países que investiram consideravelmente nas tecnologias da informação no sistema educacional não tiveram nenhuma melhoria notável dos resultados nas avaliações de compreensão da escrita, matemáticas e ciências do PISA.
"Os sistemas escolares devem encontrar soluções mais eficazes para integrar as novas tecnologias no ensino e no aprendizado", afirma Andreas Schleicher, da direção de educação e competências da OCDE.
domingo, 13 de setembro de 2015

É preciso ter a abertura do saber. Todas as coisas na vida – da sua vida – vêm para ensinar você. Não existe nenhuma situação que não traga um ensinamento. Não existe sequer uma pessoa que passou na sua vida, que não tenha vindo para ensinar você.
Você chama as pessoas. Você chama os ensinamentos. Você provoca aquilo que se manifesta na sua vida. Você compartilha aquilo que se manifesta na sua vida. Você tem total interação com todos os fatos da vida, com todas as circunstancia – boas ou ruins.
A sua energia está no bem. A sua energia está no mal.
E as pessoas que estão no seu caminho, refletem o seu bem e refletem igualmente o seu mal.
Aqueles que estão despertos para o espiritual, sabem que não há vítima, não há algoz. E tão pouco não há um mal que prevaleça, nem um bem que dure para sempre.
As energias – as situações do mundo – estão em constante oscilação. Elas são como um Céu cheio de nuvem. Você olha... E se ficar assistindo as nuvens, verá os movimentos que se formam. E nenhum controle aparente, você tem desses movimentos. Mas, você tem o seu olhar e você tem a sua permanência.
Não culpe as pessoas. As pessoas não são erradas na sua vida, ainda que elas tenham atitudes contrárias ao bem comum – aquilo que você espera delas – e, até a consciência de moralidade e do que é correto.
As pessoas são o que elas são. Mas, estão na sua vida, pelo emaranhado kármico criado por você. E estão fora da sua vida, também pelo emaranhado kármico criado por você.
Veja: que cada situação, cada pessoa, é um aprendizado.
Então, se perdoe, perdoe os outros também. E compreenda, que algo ali você teve que aprender. E se você aprendeu, abra o coração e confie no Universo, em Deus, na manifestação do Divino. Para que essa manifestação traga para você aquilo que você pode viver, em alegria, harmonia e amor.
Alguns querem apenas a felicidade. E neste mundo onde existe: o claro/escuro; a noite/o dia... A felicidade sempre estará atrelada a uma decepção ou a uma tristeza.
Quanto mais conectado você estiver, com o seu Eu Divino – com a sua consciência – menos sujeito as oscilações você estará. E a vida se tornará muito mais fácil de ser vivida. O Bom mais prolongado, e tudo aquilo que não é bom: compreendido e pacificado dentro de você.
Quando você ama, você compreende até o ato de desamor de alguém... A incompreensão, a consciência ainda não desperta, as fragilidades humanas.
Só o amor ensina. Só o amor promove a elevação, e consequentemente, a libertação. Quando – você ama a si mesmo, e compreende que existem os enganos, as incompreensões – você libera. E toda a energia dentro de você, se solta.
 E assim, você vence o karma. Não como um lixo que passa pela sua vida, mas, por um aprendizado vencido, transformado, aberto, evoluído.
E assim, você vence o karma. Não como um lixo que passa pela sua vida, mas, por um aprendizado vencido, transformado, aberto, evoluído.
Receba as nossas bênçãos e o nosso amor. Tenham paz.
Eu Sou Mestra Rowena. E venho oferecer a vocês a energia da Chama Rosa – a energia do Amor – porque, só através do amor, nós somos capazes de compreender a ação do Divino.
Estou sempre presente, para aqueles que me acolhe. Trabalho na energia, que constantemente, espalha o amor na vida das pessoas.
Você chama as pessoas. Você chama os ensinamentos. Você provoca aquilo que se manifesta na sua vida. Você compartilha aquilo que se manifesta na sua vida. Você tem total interação com todos os fatos da vida, com todas as circunstancia – boas ou ruins.
A sua energia está no bem. A sua energia está no mal.
E as pessoas que estão no seu caminho, refletem o seu bem e refletem igualmente o seu mal.
Aqueles que estão despertos para o espiritual, sabem que não há vítima, não há algoz. E tão pouco não há um mal que prevaleça, nem um bem que dure para sempre.
As energias – as situações do mundo – estão em constante oscilação. Elas são como um Céu cheio de nuvem. Você olha... E se ficar assistindo as nuvens, verá os movimentos que se formam. E nenhum controle aparente, você tem desses movimentos. Mas, você tem o seu olhar e você tem a sua permanência.
Não culpe as pessoas. As pessoas não são erradas na sua vida, ainda que elas tenham atitudes contrárias ao bem comum – aquilo que você espera delas – e, até a consciência de moralidade e do que é correto.
As pessoas são o que elas são. Mas, estão na sua vida, pelo emaranhado kármico criado por você. E estão fora da sua vida, também pelo emaranhado kármico criado por você.
Veja: que cada situação, cada pessoa, é um aprendizado.
Então, se perdoe, perdoe os outros também. E compreenda, que algo ali você teve que aprender. E se você aprendeu, abra o coração e confie no Universo, em Deus, na manifestação do Divino. Para que essa manifestação traga para você aquilo que você pode viver, em alegria, harmonia e amor.
Alguns querem apenas a felicidade. E neste mundo onde existe: o claro/escuro; a noite/o dia... A felicidade sempre estará atrelada a uma decepção ou a uma tristeza.
Quanto mais conectado você estiver, com o seu Eu Divino – com a sua consciência – menos sujeito as oscilações você estará. E a vida se tornará muito mais fácil de ser vivida. O Bom mais prolongado, e tudo aquilo que não é bom: compreendido e pacificado dentro de você.
Quando você ama, você compreende até o ato de desamor de alguém... A incompreensão, a consciência ainda não desperta, as fragilidades humanas.
Só o amor ensina. Só o amor promove a elevação, e consequentemente, a libertação. Quando – você ama a si mesmo, e compreende que existem os enganos, as incompreensões – você libera. E toda a energia dentro de você, se solta.
 E assim, você vence o karma. Não como um lixo que passa pela sua vida, mas, por um aprendizado vencido, transformado, aberto, evoluído.
E assim, você vence o karma. Não como um lixo que passa pela sua vida, mas, por um aprendizado vencido, transformado, aberto, evoluído.Receba as nossas bênçãos e o nosso amor. Tenham paz.
Eu Sou Mestra Rowena. E venho oferecer a vocês a energia da Chama Rosa – a energia do Amor – porque, só através do amor, nós somos capazes de compreender a ação do Divino.
Estou sempre presente, para aqueles que me acolhe. Trabalho na energia, que constantemente, espalha o amor na vida das pessoas.
fonte: http://mariasilviaporlovas.blogspot.com.br/2015/09/aqueles-que-sao-os-seus-melhores.html?utm_source=feedburner&utm_medium=feed&utm_campaign=Feed:+mariasilviaorlovas+(Maria+Silvia+Orlovas)
quarta-feira, 27 de maio de 2015
terça-feira, 17 de março de 2015
terça-feira, 10 de março de 2015
quinta-feira, 26 de fevereiro de 2015
quarta-feira, 25 de fevereiro de 2015
sábado, 21 de fevereiro de 2015
sexta-feira, 20 de fevereiro de 2015
Aprenda adição algébrica de números inteiros
Introdução
A curiosidade de alguns estudantes tanto do ensino fundamental ou médio sobre a história dos números e especialmente a dos números negativos, incentivou-me a pesquisar sobre o assunto, e daí surgiu a idéia de neste artigo caminhar na linha do tempo de 300 a .C. ao século XX.
Mostrando que entre a aparição e aceitação do número negativo levou mais de 1000 anos.
É interessante que os alunos saibam que as mesmas dúvidas que aparecem hoje no contato com os números inteiros, já instigava questionamentos de célebres matemáticos como Euler, Laplace, Cauchy, Mac Laurin e Carnot, por exemplo.
Laplace (1749-1827) com respeito a Regra de Sinais disse:
"É difícil conceber que um produto de (-a) por (-b) é o mesmo que a por b".
Mac Laurin (1698-1746) disse a respeito do número negativo: "A quantidade negativa, bem longe de ser rigorosamente menos que nada, não é menos real em sua espécie que a quantidade positiva".
O Surgimento do número negativo
Ao contrário dos números naturais e fracionários positivos que tem raízes em experimentações geométricas, os números negativos , os irracionais e os complexos surgiram da manipulação algébrica, como na resolução de equações de 1º e 2º graus.
Os matemáticos do período Alexandrino que se iniciou 300 a.C., influenciados pela civilização egípcia e babilônica, fizeram uma matemática mais orientada para resolver problemas práticos, abordavam temas de óptica, geografia, hidrodinâmica e astronomia.
Nestes trabalhos utilizaram números irracionais com aproximações e iniciaram uma álgebra sem usar a geometria. Foi Diofanto (300 à 250 a.C.) que introduziu uma notação abreviada para representar as potências e as quantidades desconhecidas e abordou a resolução das equações algébricas sem recorrer à geometria.
Assim o produto concreto do tipo (x-3) (x-4) foi desenvolvido algebricamente , o que há de supor que ele conhecia a identidade algébrica (a-b) (c-d)=ac-bc-ad+bd.
É citado uma regra para este produto de diferenças que pode ser considerada como o "germem" do que pode ser chamado de regra de sinais: "Subtração por subtração dá adição".
Isto não significa que conhecesse os números negativos, pois esta regra se refere ao produto de diferenças e sempre a>b e c>d , e não há produto de números negativos. Diofanto considerava somente as raízes positivas das equações, mostrando o seu desconhecimento pelos números negativos.
Civilização hindu - Invenção do
número negativo
A grande contribuição dos hindus para a matemática foi a criação de um sistema de numeração posicional de base dez, cuja eficácia e simplicidade para o cálculo aritmético se estendera universalmente.
A necessidade de agilizar os cálculos astronômicos os sábios hindus se preocupavam por idealizar formas de representação numérica que simplificassem esse cálculos.
Os matemáticos hindus mostraram ser virtuosos no cálculo aritmético e algébrico que permitiram conceber um novo tipo de símbolo para representar dívidas que posteriormente o Ocidente chamariam de negativo.
A primeira vez que explicitamente as regras que regem a aritmética com os números negativos aparecem em uma obra foi na do matemático Brahmagupta que data do ano 628 d.C. Não só utilizou os negativos em seus cálculos como os considerou entidades separadas e os dotou de uma aritmética concordante com a dos inteiros.Muitos séculos se passaram para que o interesse pelos números negativos fosse retomado.
Civilização árabe - Os negativos
ignorados
O ano de 622 d.C. marca o início da era muçulmana e o começo da expansão do estado islâmico. Após um século os árabes começaram a se interessar pela cultura dos povos conquistados.
Al-Kwrizmi foi um matemático que alcançou maior popularidade, morrendo em 850 d.C.
Ele escreveu tratados de astronomia, livros de álgebra e aritmética que tiveram muita influência na matemática européia no final da Idade Média e no Renascimento.
Alguns historiadores escreveram que foram problemas com dinheiro que interpretaram o número negativo como perda.
Negativo - esta palavra pode ter vindo desta época que eram os valores NEGADOS quando se obtinha raízes negativas de uma equação.
Renascimento
No Renascimento abriu-se uma nova etapa para os números negativos.
Provavelmente foi no Renascimento que apareceu um número negativo ligado à uma equação algébrica, na obra do matemático francês Nicolás Chuquet (1445-1500). Se trata de seu "Triparty", escrita em 1484, que poderíamos dizer hoje 4x = -2 . Não existia os símbolos "x", "=", "-".
Stevin (1548-1620) aceita os números negativos como raízes e coeficientes de equações.
Admite a adição de x +(-y) em lugar de considerá-la como subtração de y á x. Também tratou de justificar geometricamente a regra de sinais fazendo uso da identidade algébrica: (a-b) (c-d)= ac-bc-ad+bd
| b | a | ||||||
| c | |||||||
| d | |||||||
Foi o matemático Albert Girard (1590-1639) o primeiro a reconhecer explicitamente a utilidade algébrica de admitir as raízes negativas e imaginárias como soluções formais das equações; porque ele permitia uma regra geral de resolução na construção de equações através de suas raízes.
No final do século XVII, surgiu a obra de Viéte, esta mais tarde ampliada admitiu que as expressões literais pudessem tomar valores negativos, no entanto, a Álgebra não teria conhecido um tal avanço se esta generalização do número não tivesse sido acompanhada por uma descoberta igualmente fundamental, realizada em 1591 por Viéte e aperfeiçoada em 1637 por Descartes: a notação simbólica literal.
Demonstração das Regras de Sinais para
a multiplicação- Cauchy
1) a=+A 3) +a=+A 5) –a=-A
2) b=-A 4) +b=-A 6) –b= +A
Substituindo 1 em 3 temos:
+(+A) = +A + . + = +
Substituindo 2 em 4 temos:
+(-A) = -A + . - = -
Substituindo 1 em 5 temos:
-(+A)=-A - . + = -
Substituindo 2 em 6 temos:
-(-A)=+A - . - = +
A legitimidade dos números negativos deu-se definitivamente por Hermann Hankel (1839-1873) publicada em 1867, "Teoria do Sistema dos números Complexos". Hankel formulou o princípio de permanência e das leis formais que estabelece um critério geral de algumas aplicações do conceito de número.
Finalmente Dedekind (1831-1916), amigo de Cantor estabeleceu uma relação de equivalência entre pares de números naturais e faz referência da subtração como inversa da adição: a-b =c-d, logo a+d= b+d . Ele demonstra que esta relação é de equivalência, e o conjunto das classes de equivalência será o conjunto dos números Inteiros.
Foram os complexos os últimos a obterem legitimidade.
A fundamentação dos números complexos foi proporcionada por Hamiltom (1805-1865).
Profª Leda Maria Bastoni Talavera tem especialização em Educação Matemática pelas Faculdades Oswaldo Cruz leciona no Colégio Campos Salles (S.P.). Este artigo surgiu da reflexão coletiva do grupo de pesquisa em Educação Matemática da Escola do Futuro (USP), coordenado pela Drª Ruth Ribas Itacarambi.
quinta-feira, 19 de fevereiro de 2015
Espelhos e caleidoscópios: investigações matemáticas sobre simetrias
A beleza dos caleidoscópios e a possibilidade de formar inúmeras figuras quando unimos dois ou três espelhos fascinaram os alunos e os ajudaram a entender a geometria. Por meio de experiências com espelhos, o professor propôs que a turma entendesse, na prática, o conceito de simetria e as relações entre ângulos e lados de polígonos. As atividades começaram com uma pequena avaliação escrita individual para checar os conhecimentos da turma. Em seguida, Rodrigues dividiu a sala em grupos e deu início às experiências.
http://www.fvc.org.br/educadornota10/vencedores/edson-tho-rodrigues-675982.shtmlPlano cartesiano na arquitetura
Nomeado em referência ao filósofo francês René Descartes
(1596-1650), o plano cartesiano é um sistema de localização de pontos
usado em diversos contextos, por exemplo, na elaboração de gráficos, no
planejamento de construções – em plantas arquitetônicas – e como base
para serviços de GPS. Foi esse conteúdo de geometria analítica que os
alunos do 8º ano do CEEMF Vale do Saber, em Apucarana, a 362 quilômetros
de Curitiba, aprenderam com a professora nota 10 Marlene Garcia Alves.
Neste vídeo, Roberto Alfredo Pompeia, professor da Universidade
Anhembi-Morumbi, explica como o sistema de coordenadas cartesianas se
aplica à Arquitetura.
Por que a multiplicação de números com sinais iguais resulta num número positivo e de sinais diferentes num negativo?
Multiplicar números de sinais contrários sempre nos leva para o lado esquerdo do zero, ou seja, para resultados negativos. Se multiplicarmos números de sinais iguais, mesmo que estejamos à esquerda do zero, vamos procurar o oposto, que estará do lado direito.
Ilustração: Erika Onodera
A confusão com a regra dos sinais surge da atribuição de um sentido ao
resultado negativo. Afinal, contar duas ovelhas é fácil, mas como
explicar "menos duas ovelhas"? Os números negativos já foram denominados
falsos, absurdos e fictícios pelos matemáticos, pois não era fácil
vinculá-los a um objeto ou a uma situação simples como a enumeração. No
século 18, usando a reta numerada, com números à direita e à esquerda do
zero, isso foi resolvido: ficou claro que um número menor que zero,
portanto negativo, está localizado à esquerda dele, e os positivos, à
direita. Um número negativo é, portanto, oposto ao positivo. Logo,
calcular -5 +3 é o mesmo que sair do zero, andar cinco casas à esquerda
e, depois, percorrer mais três à direita, resultando -2. Já no caso de
-2 X +3, saímos do zero e andamos duas casas à esquerda por três vezes,
chegando ao -6. Finalmente, quando fazemos -2 X -3, estamos tentando
descobrir o produto de dois números opostos. Nesse caso, ao negar uma
negação, temos uma afirmação: o resultado, 6, necessariamente é
positivo.
Fonte: http://revistaescola.abril.com.br/matematica/fundamentos/multiplicacao-numeros-sinais-iguais-resulta-num-numero-positivo-sinais-diferentes-num-negativo-502930.shtml
sexta-feira, 13 de fevereiro de 2015
Jovem calcula por que é tão difícil encontrar uma namorada
Cientista movido por uma natural angústia masculina calculou quantas almas gêmeas em potencial você pode ter por aí – e mostra como é difícil encontrá-las
por Redação Galileu
 A galera da foto deu sorte - podem demorar anos até encontrar uma namorada bacana // Crédito: Shutterstock
A galera da foto deu sorte - podem demorar anos até encontrar uma namorada bacana // Crédito: Shutterstock
 A galera da foto deu sorte - podem demorar anos até encontrar uma namorada bacana // Crédito: Shutterstock
A galera da foto deu sorte - podem demorar anos até encontrar uma namorada bacana // Crédito: Shutterstock
Um cientista da computação da Universidade de Toronto chamado Tristan Miller resolveu descobrir porque é tão difícil arranjar uma namorada. Afinal, há muitos peixes no mar, não é? Ao que parece, nem tanto. Pelo menos é isso o que mostra a estatística.
Ele começa usando o número de pessoas na Terra – 7 bilhões de pessoas. Destas, 3,4 bilhões são mulheres, segundo o censo de 2010 da ONU. Ainda assim é um número alto, não? Lógico, temos que considerar a geografia. Então são 635 milhões de mulheres de países que ele pode conhecer ou que tem condições financeiras de visitá-lo em Toronto. Mas essas são todas as mulheres desses países – desde as recém-nascidas até as vovós. Supondo que você queira uma namorada com idades entre 18 e 25 anos, o número é de 68,22 milhões de mulheres.
Levando em consideração os parâmetros individuais do que é beleza, você deve se sentir atraído por 1,4 milhão destas mulheres. Mas não é só isso que você procura no amor da sua vida, né? Aquelas que vão conseguir manter um papo bacana com você, que têm as mesmas referências, são 236 mil.
Ok, mulheres na mais tenra idade, bonitas e inteligentes. É claro que uma boa parte delas já estará comprometida. Sem base no censo e sim em um ‘chute’ científico, Tristan estima que 50% delas já seja casada ou tenha namorado, o que o deixa com 118 mil possíveis namoradas.
E outro fator muito importante: a candidata também precisa te achar atraente e gostar de você. Usando os mesmos cálculos citados anteriormente para o outro lado do jogo, Tristan estima que 15.8655% dessas mulheres, ou seja, 18,726, corresponderiam seus sentimentos.
Aí temos uma quantidade de mulheres em seus padrões que também pensam o mesmo de você. Bacana – ou nem tanto. Afinal, quantas delas o acaso vai realmente permitir que você conheça? E, supondo que você vá a um encontro com cada uma delas para decidir qual é o amor da sua vida, durante todos os dias da semana, 3,493 semanas seriam gastas nesse processo todo. Isso equivale a 67 anos de busca. Se você já tem mais que 18 anos, quando você chegar lá, apostamos que as gatinhas já não vão se interessar tanto por você – isso se você ainda estiver entre os vivos.
A conclusão? A incerteza masculina sobre a mulher ideal que torna tão difícil encontrar uma namorada bacana. E outra, acrescentada pela equipe da Galileu:se o cara faz esse tipo de contas como passatempo em vez de sair por aí, não é mistério que ele ainda não tenha arranjado uma namorada.
Matemáticos criam fórmula para a decoração 'perfeita' de árvore de Natal
Objetivo é ter os enfeites colocados de forma harmoniosa.
Instrução de cálculo foi elaborada em universidade britânica.
Decorar sua árvore de Natal não é necessariamente uma questão de bom gosto. Matemáticos da Universidade de Sheffield, no Reino Unido, desenvolveram uma fórmula para você acertar na decoração de fim de ano.
Mais especificamente, ela calcula qual a proporção de ornamentos e
luzes que deixará sua árvore de Natal mais agradável de se ver.
Tudo o que você precisa saber sobre sua árvore é a altura em centímetros. Depois, é só jogar o valor na calculadora online desenvolvida pelos pesquisadores e pronto! Ela mostra quantos enfeites colocar, o comprimento do festão – na imagem, é a fita dourada que rodeia a árvore – e o tamanho ideal do pisca-pisca.
Você sabia que uma árvore de 1,80m precisa de apenas 37 ornamentos
para ficar bonitona? E pensar que ficávamos nos esforçando para enfeitar
cada galho que sobrava. Isso deveria ter chegado antes. [The University of Sheffield via PhysOrg]
Imagem: Gl0ck & Smileus/Shutterstock
Para calcular rapidinho, acesse: http://www.shef.ac.uk/news/nr/debenhams-christmas-tree-formula-1.227810
Fonte: http://g1.globo.com/natal-e-ano-novo/2012/noticia/2012/12/matematicos-criam-formula-para-decoracao-perfeita-de-arvore-de-natal.html
Assinar:
Comentários (Atom)